문제
https://school.programmers.co.kr/learn/courses/30/lessons/258705
문제 이해


이 문제는 사다리꼴 윗변에 정삼각형이 있는지를 나타내는 1차원 정수 배열 tops와 그 길이 n이 입력으로 주어진다. 도형은 돌릴 수 있으며, 문제 예시 모양을 빈틈없이 채우는 경우의 수를 반환해야한다. 도형이 다른 도형과 겹쳐서는 안된다.
제한 사항
- 1 ≤ `n` ≤ 100000
- `tops`의 길이 = `n`
- `tops[i]`는 사다리꼴의 윗변과 변을 공유하는 i + 1 번째 정삼각형의 위쪽에 정삼각형을 붙이는 경우 1, 붙이지 않는 경우 0.
문제 접근
n = 1일 경우
먼저 삼각형이 하나이고(n = 1), 사다리꼴 윗변에 정삼각형이 있는 경우(tops[0] = 1)의 경우의 수를 나눠보았다.

만약 tops[0]이 0이라면, case 2가 불가능하기 때문에, 가능한 경우의 수는 3가지가 될 것이다.

n = 2일 경우
이제 삼각형이 2개일 때(n = 2)로 확장해보자.
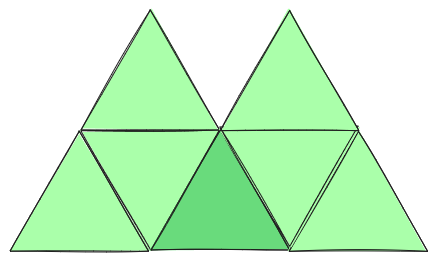
삼각형이 2개 이상일 때, 유의해야할 점은 중간에 겹치는 부분이 생긴다는 것이다.
이 부분을 어떻게 해결하느냐가 이번 문제의 포인트였던 것 같다.
나는 삼각형들을 각각 분리하여 중간이 겹칠 가능성이 있는 케이스(case 3)와, 그렇지 않은 케이스에서의 경우의 수를 따로 계산해, 합치는 방식을 사용했다.
그림으로 나타내면 다음과 같다.

n이 3이상일 때는 어떻게 나타낼 수 있을까?
위의 식으로부터, 이전 정보를 활용하는 점화식으로 만들어볼 수 있다!
점화식: 윗변에 삼각형이 있는 경우 (top = 1)

위의 식은 윗변 위에 삼각형이 있는 경우이다.
그러므로, 삼각형이 없는 경우의 점화식을 또 만들어줘야한다.
하지만 위의 식에서 크게 달라지지는 않는다!
점화식: 윗변에 삼각형이 없는 경우 (top = 0)

풀이 코드
n이 10만까지 입력으로 들어올 수 있기 때문에, DFS는 시간복잡도상 거의 불가능하다. (사실 처음에 이 방법으로 풀었었는데, 불가능했다...)
그래서, 동적 계획법(DP) 알고리즘을 사용했다.
동적 계획법은 복잡한 문제를 더 작은 하위 문제로 나누어 해결하는 알고리즘 기법이다.
하위 문제의 답을 계산하고 저장해둔 뒤, 다시 같은 문제를 만났을 때 저장해둔 값을 이용하기 때문에, 같은 계산을 여러번 반복해야하는 문제에서 효율이 좋다
function solution(n, tops) {
// n번째 삼각형이 case 0 ~ 2일 때, n번째까지의 누적 경우의 수 배열
const case0to2 = Array(n).fill(1);
// n번째 삼각형이 case 3일 때, n번째까지의 누적 경우의 수 배열
const case3 = Array(n).fill(1);
// 첫 번째 삼각형에서 가능한 case의 개수
case0to2[0] = tops[0] ? 3 : 2;
case3[0] = 1;
for(let i = 1; i < n; i++) {
if(tops[i]){
case0to2[i] = (case0to2[i - 1] * 3 + case3[i - 1] * 2) % 10007
} else {
case0to2[i] = (case0to2[i - 1] * 2 + case3[i - 1]) % 10007
}
// case 3의 경우, 삼각형 존재여부와 관계없이 동일
case3[i] = (case0to2[i - 1] + case3[i - 1]) % 10007
}
// 현재 삼각형이 case 0 ~ 2인 누적 경우의 수 + case 3인 누적 경우의 수
return (case0to2[n - 1] + case3[n - 1]) % 10007;
}